Один простой пример - и вы забудете о линейке: математик показал, как быстро измерить любое расстояние

Представим типичную ситуацию: вы готовитесь к празднику и хотите создать уютную атмосферу во дворе. Есть два здания - одно выше, 9 метров, другое ниже, 3 метра. Между ними - ровно 8 метров. Идея проста: натянуть гирлянду от вершины одного здания до вершины другого, чтобы она сияла ночью над двором.

Но возникает вопрос: какой длины должна быть гирлянда, чтобы она хорошо легла, не провисала и не оказалась короткой? Измерить ее рулеткой вряд ли получится - надо лезть на крышу, дотягиваться, рискуя равновесием. И здесь на помощь приходит математика.

В Сніданку з 1+1 учитель математики Владислав Бондаренко показал, как создать треугольник между вершинами зданий и линией, которая соединяет их по горизонтали.

«Мы создаем в воображении прямоугольный треугольник. Один катет - горизонтальное расстояние между домами, второй - вертикальная разница в высоте. Далее подставляем в формулу и считаем», - пояснил учитель.

Один катет - это 8 метров (расстояние между зданиями), второй - 6 метров (разница высот между зданиями: 9 - 3).

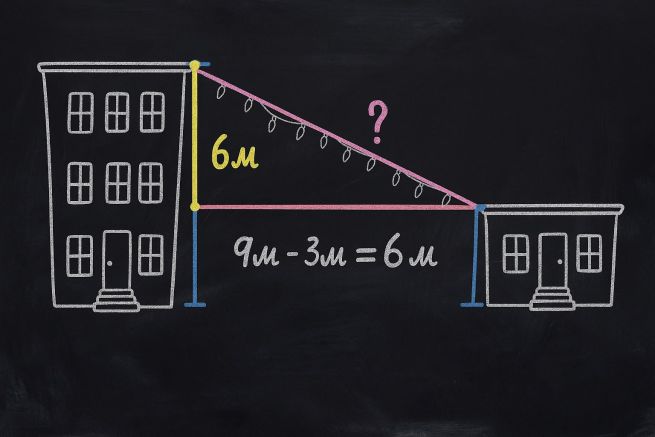
Гипотенуза же - это наша гирлянда. А чтобы ее найти, надо вспомнить теорему Пифагора:

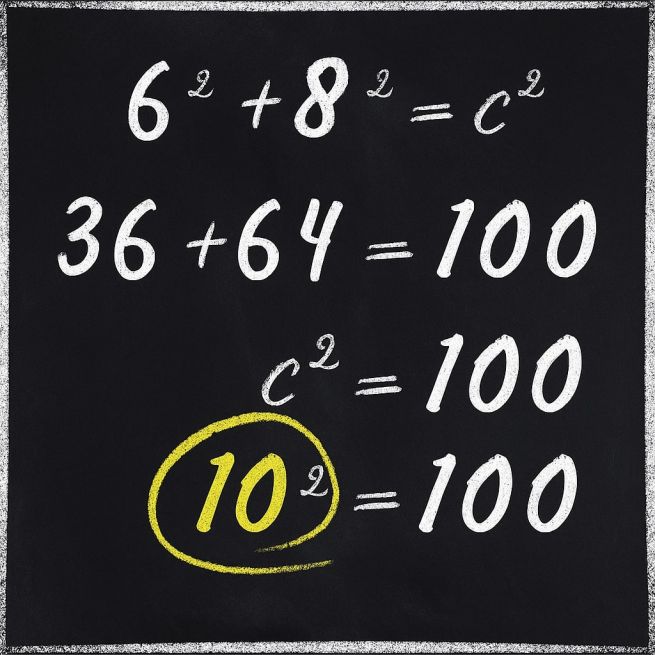
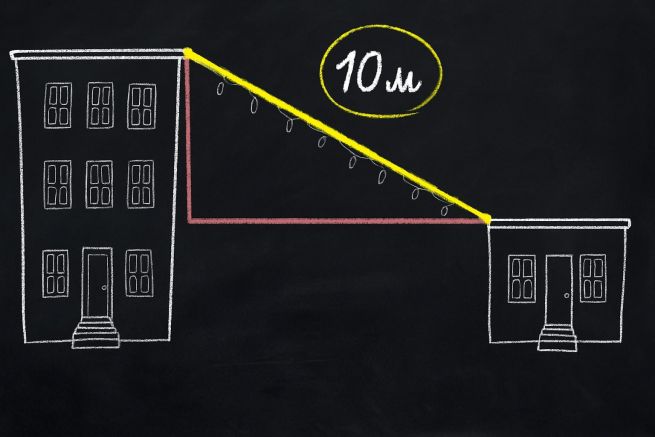
Интересно, что древние египтяне не знали о формуле Пифагора, но уже активно использовали подобные соотношения в строительстве. Они пользовались так называемым треугольником 3-4-5 - если сделать треугольник из отрезков 3, 4 и 5 метров, то он точно будет прямоугольным. А значит, можно легко создать угол 90 градусов, например, во время ремонтных или строительных работ.

ЧИТАЙТЕ ТАКЖЕ: Когда 10% выгоднее 11%: математик объяснил, как на самом деле работает депозит и как посчитать проценты, чтобы не потерять деньги